一、计算器的计算思路分析
我们以计算3+8*2-6这个算式为例:
将算式解析为数字和符号:
3,+,8,*,2,-,6准备一个用于存放数字的数字栈numStack,还有一个存放运算符号的符号栈symbolStack,下面分别简称栈n和栈s
按顺序扫描解析后的数字和符号,
如果是数字,就直接入数栈n,
如果是符号,且如果符号栈s为空,就直接入栈,
如果s不为空,就需要比较栈顶符号与当前符号的优先级,再分两种情况:
- 如果栈顶符号优先级比当前符号大,就从栈n弹出两个数字,从栈s弹出一个符号,然后进行运算,最后得出的结果再入栈n
- 如果栈顶符号优先级小于或等于当前符号,就将符号入栈s
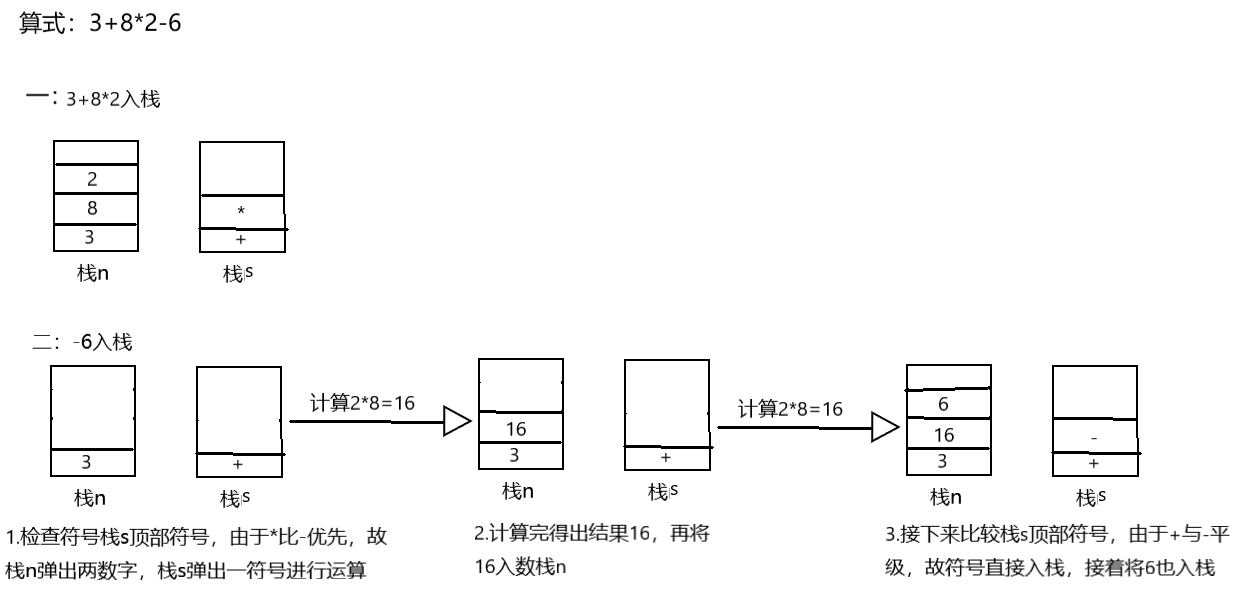
按照这个流程,扫描完后栈n会留下3,16,6这三个数,栈s会留下+,-这两个 符号,
然后按顺序,栈n弹出两个数字,栈s弹出一个符号,然后运算得到结果后再入栈n,重复此步骤,最后栈s清空,栈n只剩一个数字,即为运算结果。
二、代码实现
我们先来实现一个加减乘除的数计算器:
1 | /** |
现在输入运算公式调用calculate()函数即可得出结果,但是目前这个计算器仍然还有致命问题没有解决:
当连续乘除时无法识别,比如:2*3*3+3会被识别为(2*3)*(3+3),
这个问题下面我们将用递归来解决。
三.、使用递归解决连乘问题
我们分析主函数calculate()中关于比较符号的代码片段:
1 | //如果是符号就比较符号优先级 |
可以知道主要问题在于运算符的比较只能进行一次,实际上可能会有连需乘除的情况。
举个例子,要计算1*2*3*4+3,+入栈前,数字栈有1234,符号栈有三个*:
- 加号入栈前,取出第一个乘号比较,发现乘法优先,于是取出4和3乘后得12,把12入数栈
- 此时数栈有1,2和12,符号栈有两个*,然后重复步骤1过程,再把乘号取出一个进行比较......
- 步骤2结束后数字栈有1和24,符号栈还有一个*,于是再重复步骤1过程.....
- 最终,符号栈没有比+更优先的符号了,于是加号入栈
以此类推,无论有多少个乘号,实际上的代码都是重复执行步骤1,直到满足进入步骤4的条件时结束。
如果我们把步骤1提取成一个函数,让他执行结束后再调用自己,有几个乘号就让他自己调用几次,那么等到满足步骤4的条件时,也就说明套娃到底了,这时就可以结束调用返回结果。
按照这个思路,我们把原先的代码提取成一个递归方法:
1 | /** |
现在就能计算连续乘除的情况了!
四.完整代码
1 | /** |