数据结构与算法（七）：迷宫回溯和八皇后问题

发表于 | 分类于
字数统计: 1.9k

一、迷宫回溯问题

1.问题

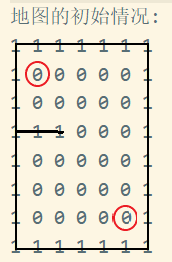
一个7*8的数组模拟迷宫，障碍用1表示，通路使用0表示，给定起点（1,1）和终点（6,5），要求给出起点到终点的通路

2.解题思路

  1. 首先，我们需要给程序一个寻向的基本策略，我们先假定寻向顺序为“下-右-上-左”，也就是说从起点出发，先往下走，往下走不通就往右.....以此类推
  2. 然后我们需要给走过的路一个标记，暂记为2
  3. 而当从一个方向走到一个只能原路返回的死胡同时，就给这段路标记为3
  4. 当抵达终点坐标（6,5）时程序结束

3.代码实现

3.1生成地图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * 创建一个二维数组,用于模拟8*7迷宫
 * 使用1表示不可通过的实心方块，0表示可通过砖块
 * （6,5）为默认终点，（1,1）为默认起点
 * @return
 */
public static int[][] getMap(){
    int[][] map = new int[8][7];
    //上下全置为1
    for(int i = 0;i <7 ;i++){
        map[0][i] = 1;
        map[7][i] = 1;
    }
    //左右全置为1
    for(int i = 0;i < 8;i++){
        map[i][0] = 1;
        map[i][6] = 1;
    }
    //设置挡板
    map[3][1] = 1;
    map[3][2] = 1;

    //输出地图
    System.out.println("地图的初始情况:");
    showMap(map);

    return map;
}

/**
 * 展示地图
 * @param map
 */
public static void showMap(int[][] map) {
    for(int i = 0;i < 8;i++){
        for(int j = 0;j < 7;j++){
            System.out.print(map[i][j] + " ");
        }
        System.out.println();
    }
}

3.2 寻路逻辑的实现

对于这个寻路程序，我们可以看见，往四个方向走的过程实际上除了方向外动作上是一样的；而具体分析同一个方向，每走过一个坐标的动作也是一样的，我们对流程进行分析：

  1. 出发，先往下走，判断下一格有没有障碍（int[x][y]==1）
  2. 如果没有障碍，就继续往下走，然后重复步骤1到碰到障碍为止
  3. 如果有障碍，就按“下-右-上-左”的顺序，换个方向，然后重复步骤1到碰到障碍为止
  4. 如果找到了（6,5）就结束

表现为代码实际上就是一个递归的过程：

  • 找路是方法体
  • 找到了（6,5）或者死胡同是终止条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * 给定起始点，根据地图找路
 * 使用2表示可以走通的路，使用3表示走过但是不通的路
 * @param map 地图二维数组
 * @param x 起始点横坐标
 * @param y 起始点纵坐标
 * @return
 */
public static boolean findWay(int[][] map, int x, int y) {
    //如果走到了终点就终止
    if (map[6][5] == 2){
        return true;
    }else {
        //只有为0的路才能通过
        if (map[y][x] == 0) {
            //如果该点可以走通就打上标记
            map[y][x] = 2;
            if (findWay(map, x, y + 1)) {
                //向下递归
                return true;
            } else if (findWay(map, x + 1, y)) {
                //向右递归
                return true;
            } else if (findWay(map, x, y - 1)) {
                //向上递归
                return true;
            } else if (findWay(map, x - 1, y)) {
                //向左递归
                return true;
            } else {
                //都走不通说明是死胡同
                map[y][x] = 3;
                return false;
            }
        }else {
            //不为0说明要么是死路要么是障碍
            return false;
        }
    }
}

3.3 运行结果

将findWay()方法中的终止条件从map[6][5] == 2换成其他坐标即可更换终点位置，

棋盘大小和障碍物位置不影响findWay()方法寻路。

二、八皇后问题

1.问题

皇后问题，一个古老而著名的问题，是回溯算法的典型案例。该问题由国际西洋棋棋手马克斯·贝瑟尔于 1848 年提出：

在 8×8 格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，求有多少种摆法？

2.解题思路

  1. 首先，我们先使用一个长度为8数组来表示八皇后的摆放位置，数组下标+1即表示棋盘的第几行，数组下标对应的存放的数字+1即为棋盘的第几列。举个例子：

    arr = {0,2,3,8,4,6,2,7}

    其中，元素0下标为0，即表示第一行第一列；元素2下标为1，即表示第二行第三列......以此类推。

  2. 任意假设任意坐标分标为(x1,y1)，(x2,y2)，也就是用数组表示为arr[x1]=y1，arr[x2]=y2的两个皇后不允许在同一列，我们可以理解为：

    arr[x1] != arr[x2];

    而任意坐标的皇后不允许在同一斜线，即(x2-x1)=(y2-y1)，也就是斜率不应当相同，我们可以理解为：

    Math.abs(x2-x1) != Math.abs(arr[x2]-arr[x1])

    （注：Math.abs()为求绝对值方法）

3.代码实现

3.1 检查摆放位置的代码实现

在前面明确了如何用数组表示位置，以及如何检查皇后是否允许摆放后，我们有如下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//表示皇后位置的数组
int[] arr = new int[8];

/**
 * 检查第n个皇后是否与前面摆放的皇后冲突
 * @param n
 * @return
 */
public boolean check(int n) {
    //检查第n层之前的皇后位置
    for (int i = 0; i < n; i++) {
        // arr[i] == arr[n] 检查是否同一列
        // Math.abs(n - i) == Math.abs(arr[n] - arr[i]) 检查是否同一斜线
        if (arr[i] == arr[n] ||
            Math.abs(n - i) == Math.abs(arr[n] - arr[i])) {
            return false;
        }
    }
    return true;
}

3.2 完整代码

接着我们需要考虑如何使用递归方法来做到以下效果：

使用一个方法遍历第n行的每一列，检查每一列是否可以放置皇后：

  1. 如果可以放置皇后，将位置出入arr[n]中，然后递归调用自己，传入n+1开始遍历下一行.....以此类推
  2. 如果不可以放置皇后，就跳过该列检查下一列，如果可以就重复步骤1
  3. 若n行中全部位置都不合适，则结束本层返回上一层n-1层，重复步骤1
  4. 如果最后n=8，即八个皇后全部放置完毕，记一次完成摆放，然后结束递归返回第一层，继续检查第一层的下一列

最终代码实现结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
/**
 * @Author：黄成兴
 * @Date：2020-06-26 20:53
 * @Description：八皇后问题
 */
public class EightQueens {

    public static void main(String[] args) {
        EightQueens eightQueens = new EightQueens();
        eightQueens.set(0);
        System.out.println("共有摆法：" + eightQueens.count);
    }

    //记录八皇后有几种摆法
    int count = 0;

    //表示皇后位置的数组
    int[] arr = new int[8];

    /**
     * 摆放皇后
     * @param n 第几个皇后
     */
    private void set(int n) {
        //如果放置好了第8个皇后
        if (n == 8){
            show();
            //记录一种摆放方式
            count++;
            //回到第一层继续递归
            return;
        }

        //遍历第n行的每一列
        for (int i = 0; i < 8; i++) {
            //将该皇后放置在第n行第i列
            arr[n] = i;
            //检查放置位置是否合适
            if (check(n)){
                //如果位置合适，就递归找下一个（n+1）皇后的摆放位置
                set(n + 1);
            }
            //如果位置不合适，就跳过这一列检查下一列
        }
    }

    /**
     * 检查第n个皇后是否与前面摆放的皇后冲突
     * @param n
     * @return
     */
    public boolean check(int n) {
        //检查第n层之前的皇后位置
        for (int i = 0; i < n; i++) {
            // arr[i] == arr[n] 检查是否同一列
            // Math.abs(n - i) == Math.abs(arr[n] - arr[i]) 检查是否同一斜线
            if (arr[i] == arr[n] ||
                Math.abs(n - i) == Math.abs(arr[n] - arr[i])) {
                return false;
            }
        }
        return true;
    }
    

    /**
     * 展示某一摆法中八皇后的摆放位置
     */
    public void show() {
        for (int i : arr) {
            System.out.print(i + " ");
        }
        System.out.println();
    }
}
0%