什么是查找?
查找是在大量的信息中寻找一个特定的信息元素,在计算机应用中,查找是常用的基本运算,例如编译程序中符号表的查找。
定义:根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素(或记录)。
分类:
- 静态查找和动态查找
- 静态查找:不对表的数据元素和结构进行任何改变。
- 动态查找:在查找过程同时插入查找表中不存在的数据元素,或者从查找表中删除已经存在的某个数据元素。
- 无序查找和有序查找。
- 无序查找:被查找数列有序无序均可
- 有序查找:被查找数列必须为有序数列。
一、线性查找
遍历数组并且依次对比值,相等时返回下标
1 | /** |
二、二分查找
1.思路分析
- 要查找数target,首先要在给定的有序数组中找到中间位置的数,定义为arr[mid]
- 比较target与arr[mid]大小:
- target < arr[mid]:说明target元素的下标小于mid,向右查找
- target > arr[mid]:说明target元素的下标大于mid,向左查找
- target = arr[mid]:即找到了
- 递归重复以上步骤直到找到或者找不到元素为止
2.代码实现
查找不含有重复数字的情况:
1 | /** |
查找含有重复数字的情况:
1 | /** |
三、插值查找
插值查找与二分查找基本一致,但是不一样的是不再像二分那样总是将数组均匀分为两份,而是通过公式将分割的中间点自适应定在目标元素附近。

即将原先的mid计算方式换成这个:
1 | //将原先的1/2换为(key-a[low])/(a[high]-a[low]) |
由于mid的计算方式改为由查找数动态计算,所以为了防止取arr[mid]时下标越界,我们需要新的边界条件:
- 目标target不能小于有序数组最小数,即arr[0]
- 目标target不能大于于有序数组最大数,即arr[arr.length]
所以代码实现如下:
1 | /** |
四、斐波那契查找
斐波那契查找跟差值查找一样从中位数mid上下文章,但是又有不同之处,要想理解斐波那契查找的思路,需要先了解一下斐波那契数列:
举个例子, {1, 1, 2, 3, 5, 8, 13, 21, 34, 55 } 就是一个斐波那契数列,他有两个特点:
- F[k] = F[k-1] + F[k-2]
- 相邻数之比无限接近黄金分割值0.618
1.思路分析
由于F[k] = F[k-1] + F[k-2],我们能推出(F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1,也就是说:
若数组的长度F[k]-1,则每一数组可以被分成长度为F[k-1]-1和F[k-2]-1的两段,两段的平分点mid即有mid=low+F[k-1]-1
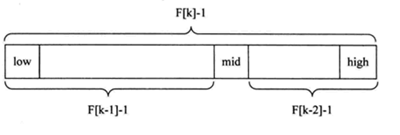
但数组长度n不一定刚好等于F[k]-1,所以需要将原来的顺序表长度n增加至F[k]-1。新增的位置(从n+1到F[k]-1位置),都赋为n位置的值即可
举个例子:延长{1,8, 10, 89, 1000, 1234},得到{1,8, 10, 89, 1000, 1234, 1234, 1234},
2.代码实现
1 | /** |