数据结构与算法（十一）：二叉树

发表于 | 分类于
字数统计: 2.1k

一、什么是二叉树

1.概述

首先，需要了解树这种数据结构的定义：

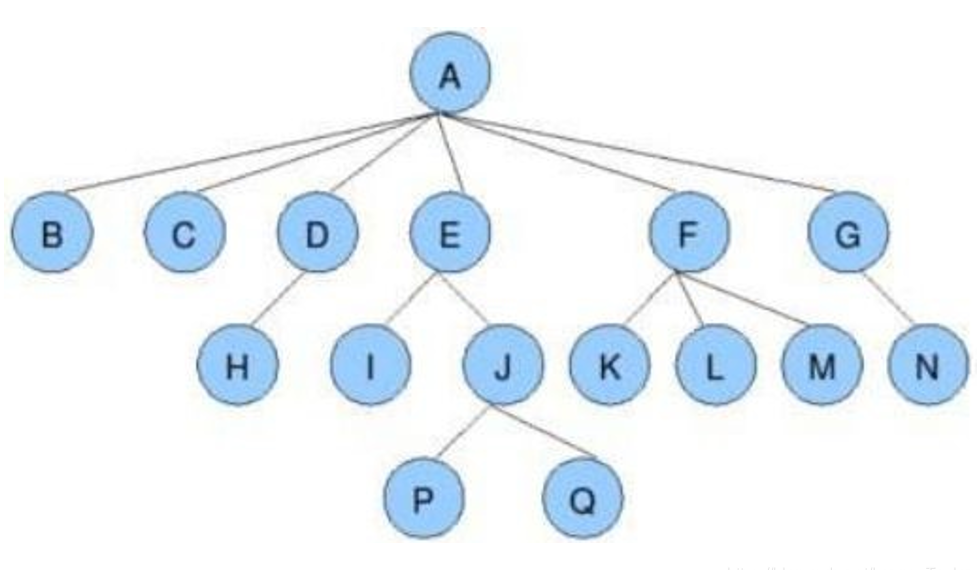
树：是一类重要的非线性数据结构，是以分支关系定义的层次结构。每个结点有零个或多个子结点；没有父结点的结点称为根结点；每一个非根结点有且只有一个父结点；除了根结点外，每个子结点可以分为多个不相交的子树

树的结构类似现实中的树，一个父节点有若干子节点，而一个子节点又有若干子节点，以此类推。

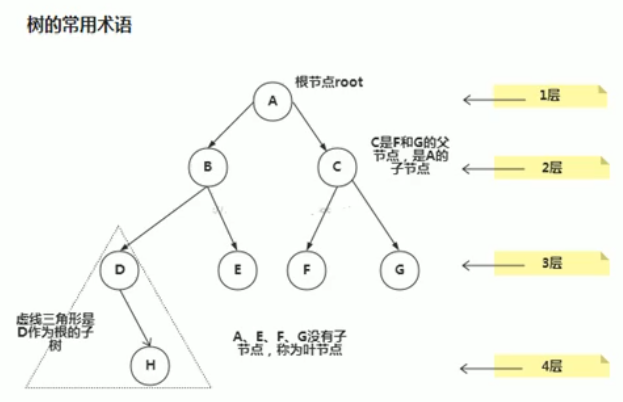
2.名词解释

名称 含义
根节点 树的顶端结点
父节点 若一个节点含有子节点，则这个节点称为其子节点的父节点
子节点 具有相同父节点的节点
兄弟节点 彼此都拥有同一个父节点的节点
叶子节点 即没有子节点的节点
节点的权 即节点值
路节点的度 一个节点含有的子树的个数
树的度 一棵树中，最大的节点的度称为树的度
深度 根结点到这个结点所经历的边的个数
层数 该节点的深度+1
高度 结点到叶子结点的最长路径所经历的边的个数
树高度 即根节点的高度
森林 由m（m>=0）棵互不相交的树的集合称为森林

3.二叉树

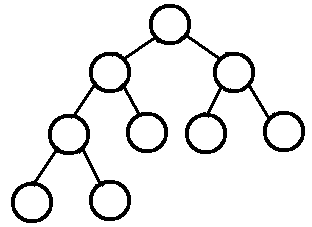
二叉树就是每个节点最多只有两颗子树的树：

对于二叉树有：

  • 满二叉树：所有的子节点都在最后一层，且节点总数与层数有节点总数=2^n-1

  • 完全二叉树：从根节点到倒数第二层都符合满二叉树，但是最后一层节点不完全充填，叶子结点都靠左对齐

二、二叉树的遍历

二叉树遍历分为三种：

  • 前序遍历: 先输出父节点，再遍历左子树和右子树
  • 中序遍历: 先遍历左子树，再输出父节点，再遍历右子树
  • 后序遍历: 先遍历左子树，再遍历右子树，最后输出父节点

可见，根据父节点输出顺序即可以判断是哪一种遍历。

1.简单代码实现

先创建节点类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
/**
 * @Author：黄成兴
 * @Date：2020-07-11 17:30
 * @Description：二叉树
 */
public class BinaryTreeNode {

    private int nodeNum;

    /**
     * 右子节点
     */
    private BinaryTreeNode right;

    /**
     * 左子节点
     */
    private BinaryTreeNode left;

    public BinaryTreeNode(int nodeNum) {
        this.nodeNum = nodeNum;
    }

    @Override
    public String toString() {
        return "BinaryTreeNode{" +
                "nodeNum=" + nodeNum +
                '}';
    }

    public int getNodeNum() {
        return nodeNum;
    }

    public void setNodeNum(int nodeNum) {
        this.nodeNum = nodeNum;
    }

    public BinaryTreeNode getRight() {
        return right;
    }

    public void setRight(BinaryTreeNode right) {
        this.right = right;
    }

    public BinaryTreeNode getLeft() {
        return left;
    }

    public void setLeft(BinaryTreeNode left) {
        this.left = left;
    }
}

实现遍历方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
/**
 * @Author：黄成兴
 * @Date：2020-07-11 17:44
 * @Description：二叉树
 */
public class BinaryTree {

    private BinaryTreeNode root;

    public BinaryTree(BinaryTreeNode root) {
        if (root == null) {
            throw new RuntimeException("根节点不允许为空！");
        }
        this.root = root;
    }

    public void preOrder(){
        preOrder(root);
    }
    /**
     * 前序遍历
     */
    public void preOrder(BinaryTreeNode node){
        //打印节点
        System.out.println(node);
        //向左子树前序遍历
        if (node.getLeft() != null) {
            preOrder(node.getLeft());
        }
        //向右子树前序遍历
        if (node.getRight() != null) {
            preOrder(node.getRight());
        }
    }

    public void inOrder(){
        inOrder(root);
    }
    /**
     * 中序遍历
     */
    public void inOrder(BinaryTreeNode node){
        //向左子树中序遍历
        if (node.getLeft() != null) {
            inOrder(node.getLeft());
        }
        //打印节点
        System.out.println(node);
        //向右子树中序遍历
        if (node.getRight() != null) {
            inOrder(node.getRight());
        }
    }

    public void postOrder(){
        postOrder(root);
    }
    /**
     * 后序遍历
     */
    public void postOrder(BinaryTreeNode node){
        //向左子树中序遍历
        if (node.getLeft() != null) {
            postOrder(node.getLeft());
        }
        //向右子树中序遍历
        if (node.getRight() != null) {
            postOrder(node.getRight());
        }
        //打印节点
        System.out.println(node);
    }
}

2.测试

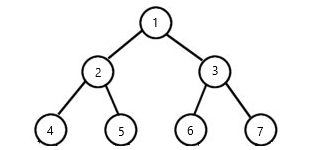
对含有7个简单的满二叉树进行遍历的结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
前序遍历：
BinaryTreeNode{nodeNum=1}
BinaryTreeNode{nodeNum=2}
BinaryTreeNode{nodeNum=4}
BinaryTreeNode{nodeNum=5}
BinaryTreeNode{nodeNum=3}
BinaryTreeNode{nodeNum=6}
BinaryTreeNode{nodeNum=7}
中序遍历：
BinaryTreeNode{nodeNum=4}
BinaryTreeNode{nodeNum=2}
BinaryTreeNode{nodeNum=5}
BinaryTreeNode{nodeNum=1}
BinaryTreeNode{nodeNum=6}
BinaryTreeNode{nodeNum=3}
BinaryTreeNode{nodeNum=7}
后序遍历：
BinaryTreeNode{nodeNum=4}
BinaryTreeNode{nodeNum=5}
BinaryTreeNode{nodeNum=2}
BinaryTreeNode{nodeNum=6}
BinaryTreeNode{nodeNum=7}
BinaryTreeNode{nodeNum=3}
BinaryTreeNode{nodeNum=1}

三、二叉树的查找

大体逻辑同遍历，这里就不在赘述了，直接放代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
/**
 * 前序查找
 * @param num
 * @param node
 * @return
 */
public BinaryTreeNode preSearch(int num,BinaryTreeNode node){
    BinaryTreeNode result = null;

    //判断当前节点是否为查找节点
    if (node.getNodeNum() == num) {
        result = node;
    }
    //判断左节点是否为空，不为空就前序查找节点
    if (node.getLeft() != null) {
        result = preSearch(num, node.getLeft());
    }
    //如果左树找到就返回
    if (result != null){
        return result;
    }
    //否则就判断并递归前序查找右树
    if (node.getRight() != null) {
        result = preSearch(num, node.getRight());
    }
    return result;
}

/**
 * 中序查找
 * @param num
 * @param node
 * @return
 */
public BinaryTreeNode inSearch(int num,BinaryTreeNode node){
    BinaryTreeNode result = null;

    //判断左节点是否为空，不为空就中序查找节点
    if (node.getLeft() != null) {
        result = inSearch(num, node.getLeft());
    }
    //如果左树找到就返回
    if (result != null){
        return result;
    }
    //如果左树未找到就判断当前节点是不是
    if (node.getNodeNum() == num) {
        result = node;
    }
    //否则就判断并递归前序查找右树
    if (node.getRight() != null) {
        result = inSearch(num, node.getRight());
    }
    return result;
}

/**
 * 后序查找
 * @param num
 * @param node
 * @return
 */
public BinaryTreeNode postSearch(int num,BinaryTreeNode node){
    BinaryTreeNode result = null;

    //判断左节点是否为空，不为空就后序查找节点
    if (node.getLeft() != null) {
        result = postSearch(num, node.getLeft());
    }
    //如果左树找到就返回
    if (result != null){
        return result;
    }

    //否则就判断并递归后序查找右树
    if (node.getRight() != null) {
        result = postSearch(num, node.getRight());
    }
    //判断右树是否找到
    if (result != null){
        return result;
    }

    //如果右树仍未找到就判断当前节点是不是
    if (node.getNodeNum() == num) {
        result = node;
    }
    return result;
}

四、二叉树的删除

对于二叉树的删除，有以下逻辑：

  • 由于树的节点和节点之间的联系是单向的，对于要删除的节点，需要找到他的父节点进行删除
  • 从根节点开始遍历节点，判断节点的左右子节点是否为目标节点
  • 如果是就删除并返回
  • 否则就持续向右或左递归，直到找到目标节点，或者将树遍历完为止
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * 删除节点
 * @param num
 * @param node
 * @return
 */
public void delete(int num, BinaryTreeNode node) {
    //判断删除的是否为根节点
    if (root.getNodeNum() == num) {
        throw new RuntimeException("不允许删除根节点！");
    }
    //如果子节点就是要删除的节点
    if (node.getLeft() != null && node.getLeft().getNodeNum() == num) {
        node.setLeft(null);
        return;
    }
    if (node.getRight() != null && node.getRight().getNodeNum() == num) {
        node.setRight(null);
        return;
    }
    //否则就往左树或右树遍历直到找到或遍历完为止
    if (node.getLeft() != null) {
        delete(num, node.getLeft());
    }
    if (node.getRight() != null) {
        delete(num,node.getRight());
    }
}

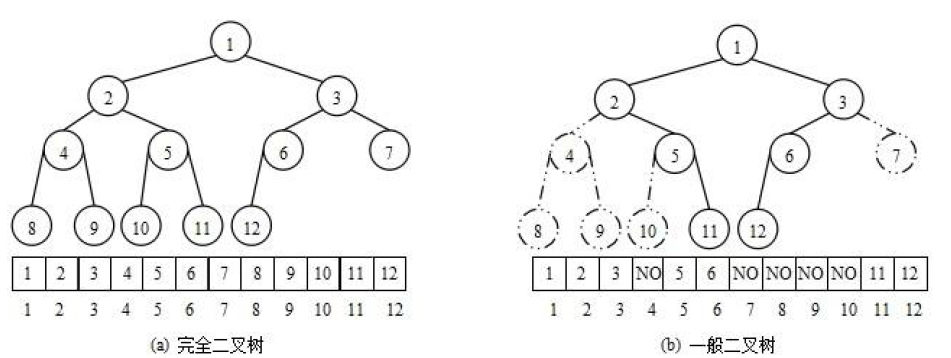
五、顺序存储二叉树

一般想到二叉树都会先想到较为形象的链式存储，即用含有左右指针的节点来组成树，实际上，通过计算，也可以使用数组来表示二叉树。

可以简单的理解：顺序存储二叉树是逻辑的上一棵树，而链式存储二叉树是物理上的一棵树。

以下图的树为例：

假设数组为{1,2,3,4,5,6,7,}，我们可以知道：

  • 下标为n的元素的左节点为：2*n+1
  • 下标为n的元素的右节点为：2*n+2
  • 下标为n的元素的父节点为：(n-1)/2

如果给顺序存储二叉树写一个前序遍历急就是这样：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * 前序遍历
 * @param index
 */
public void preOrder(int index) {
    //输出数组
    System.out.println(arr[index]);
    //向左递归
    if ((index * 2 + 1) < arr.length) {
        preOrder(index * 2 + 1);
    }
    //向右递归
    if ((index * 2 + 2) < arr.length) {
        preOrder(index * 2 + 2);
    }
}

在代码的实现上和链式二叉树是差不多的，这里就不再一一列举了。

当然，由于顺序存储二叉树的性质，当树需要排序的情况下，顺序存储二叉树就会出现空间浪费的情况：

0%