一、什么是堆排序
1.堆,堆排序
对于“堆”我们可以理解为具有以下性质的完全二叉树:
- 每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆
- 每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
在排序时,一般升序采用大顶堆,降序采用小顶堆。
2.大顶堆
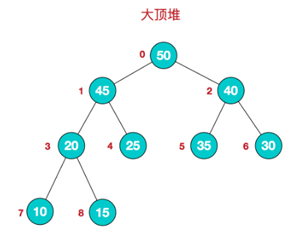
我们可以看到,层数从小到大,节点的数字是越来越小的,映射到数组有:{50,45,40,20,25,35,30,10,15}
特点是arr[i] >= arr[2*i+1] && arr[i] >= arr[2*i+2]
3.小顶堆
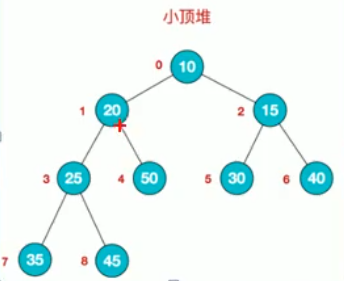
跟大顶堆相反,层数从小到大,节点的数字是越来越大,映射到数组:{10,20,15,25,50,30,40,35,45}
特点是:arr[i] <= arr[2*i+1] && arr[i] <= arr[2*i+2]
二、堆排序的思路分析
1.概述
- 将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。
- 将其与末尾元素进行交换,此时末尾就为最大值。
- 然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
- 遍历构建大顶堆,在这过程中元素的个数逐渐减少,直到最后得到一个有序序列了.
2.举个例子
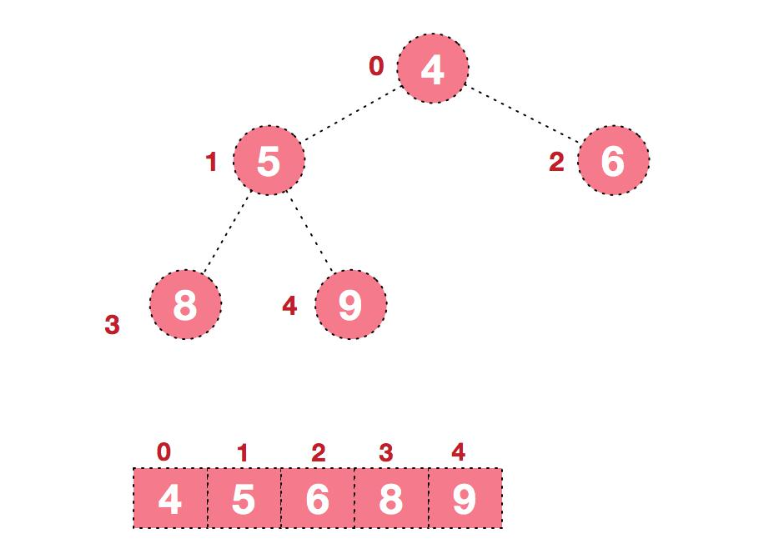
对数组{4,6,8,5,9}进行排序。
第一遍排序
我们从最后一个非叶子结点开始排序。第一个非叶子结点为
arr.length/2-1=5/2-1=1,也就是元素6.,我们对他进行对比并调整位置;
在{6,5,4}中,5比6小,而9比6大,所以9和6交换位置;
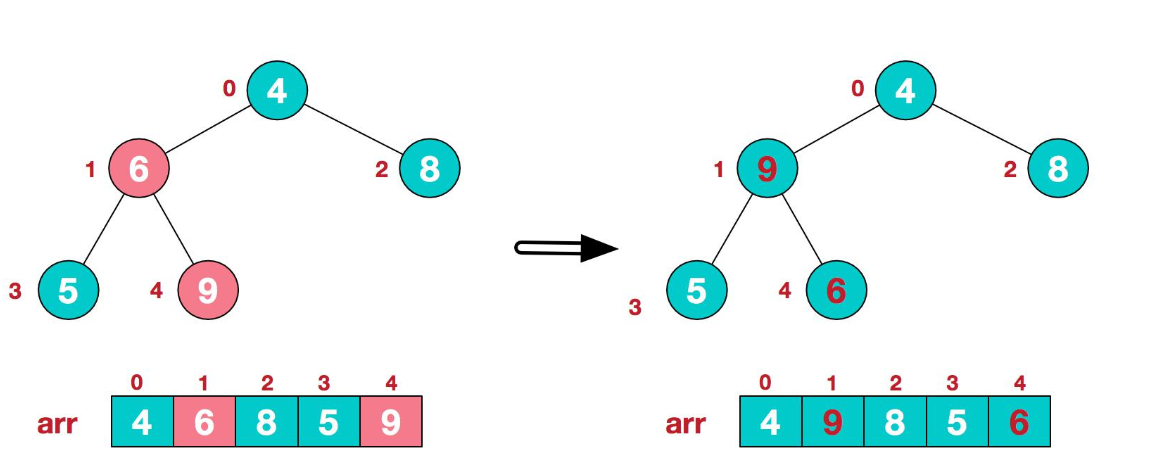
接着找到第二个非叶子节点4,由于9是{9,4,8}这个树中最大的,故9与4交换位置
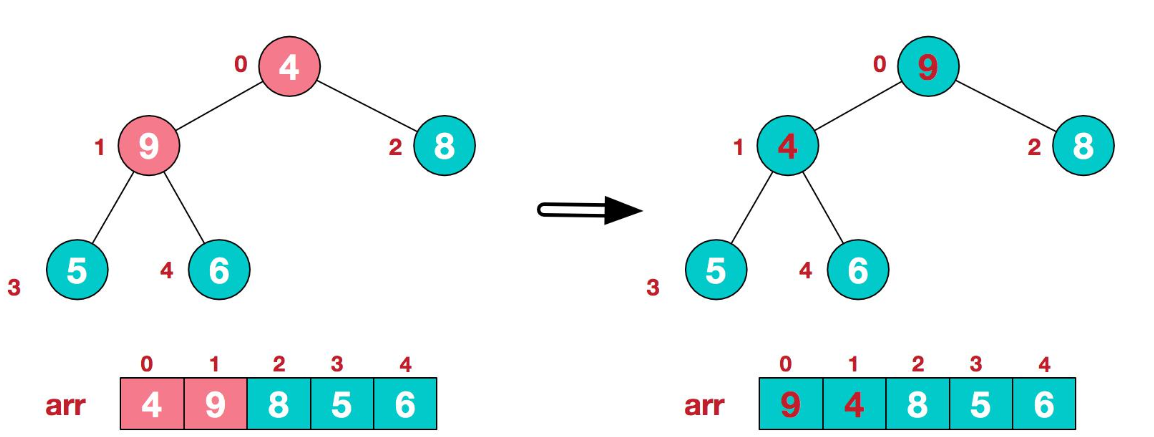
由于9与4交换位置打乱了原先{9,5,6}这棵树顺序,所以继续对新树{4,5,6}进行排序
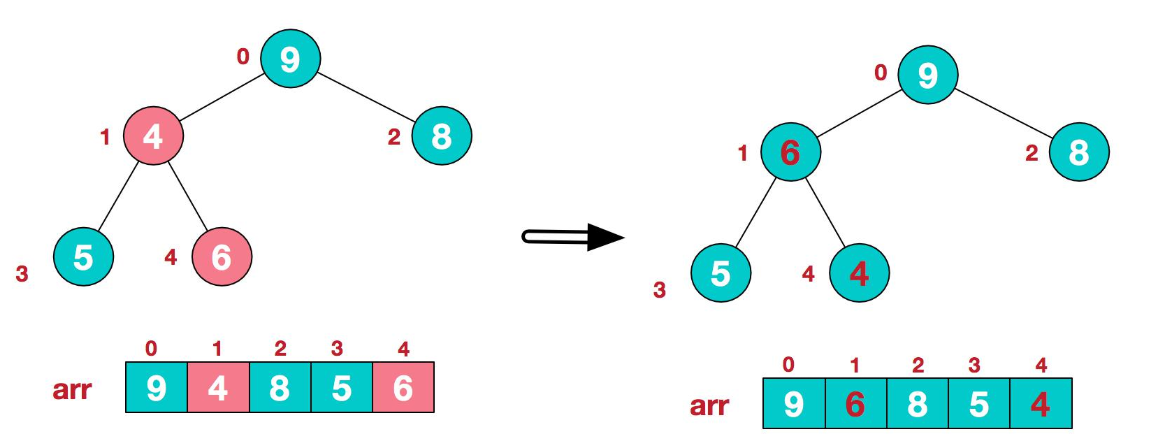
由此得到了一个大顶堆,然后将堆顶元素9与末尾元素4进行交换,得到数组{4,6,8,5,9}
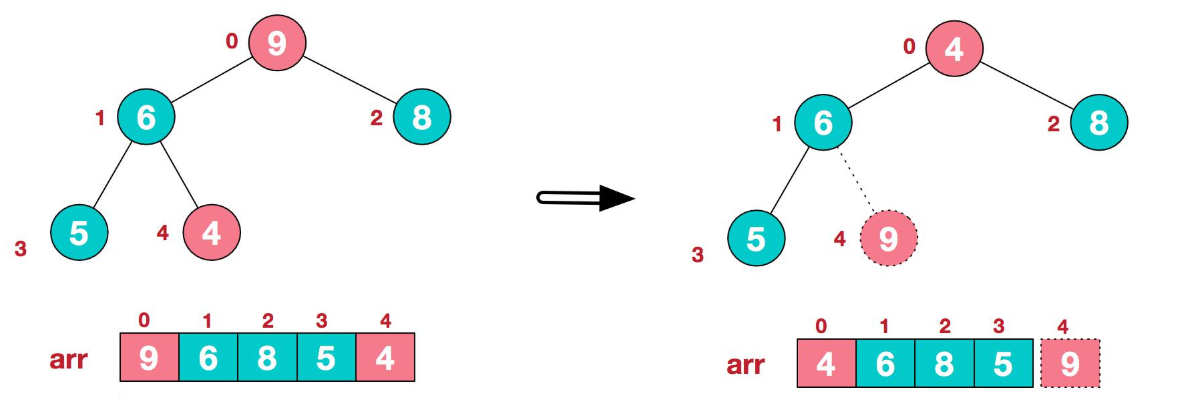
至此,第一遍排序已经完成,我们确定了最大元素9的位置
第二遍排序
第二遍排序开始时,最大元素9的位置已经确定,实际上要排序的数组变成了{4,6,8,5}
继续从6开始比较,{6,5}排序正常,所以接着比较{4,6,8},8是最大的,所以与4交换位置
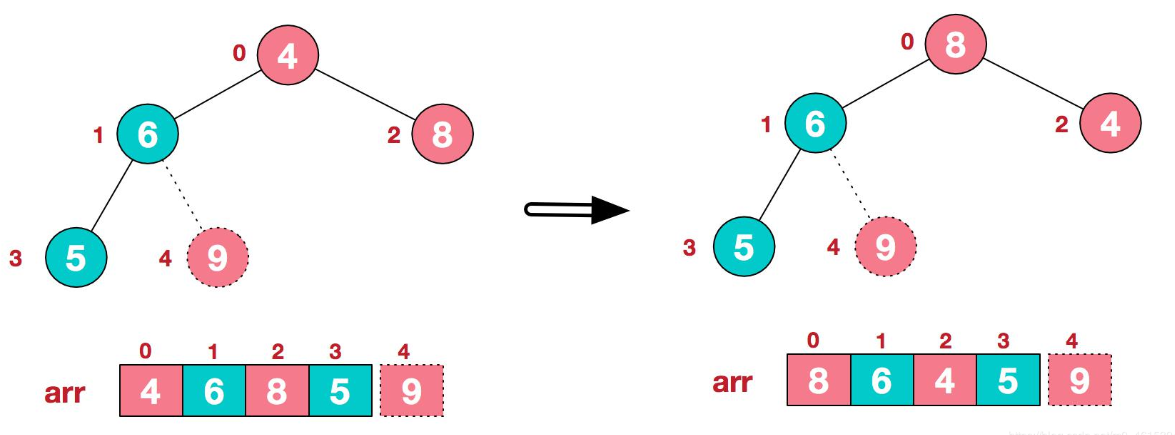
由此得到了一个大顶堆,然后将堆顶元素8与末尾元素5进行交换,得到数组{8,6,4}
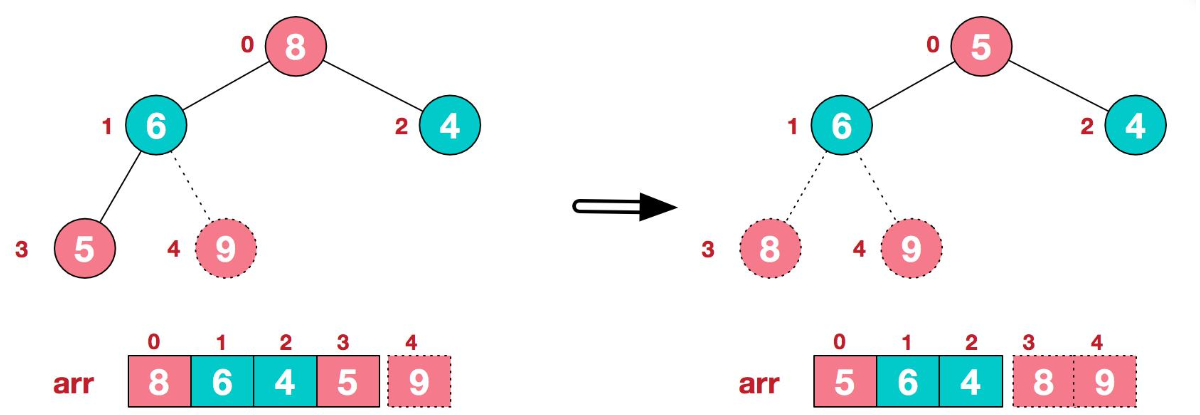
至此,第一遍排序已经完成,我们确定了最第二大元素8的位置
第三遍~第n遍排序
第二遍排序开始时,最大元素9和第二大元素8的位置已经确定,实际上要排序的数组变成了{5,6,4}
重复比较-排序-交换堆顶和队尾元素位置这一过程,直到最终获得有序数列
三、代码实现
1 | /** |