数据结构与算法（十四）：赫夫曼编码

发表于 | 分类于
字数统计: 4.5k

一、什么是赫夫曼编码

哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，

使用赫夫曼编码可以有效的压缩数据，通常可以节省20%~90%的空间。

在理解赫夫曼编码前，我们需要对通讯领域的两种编码方式有个粗略的了解。

假设我们需要传输 I'm a jvav programmer and I love programming这样一句话，我们有两种传输方式：

  1. 定长编码

    直接转换为对应长度的二进制格式

    1
    01101111 00100000 00100000 00100000 00100111 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100111 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000

    总长度为296个字符

  2. 变长编码

    按照各个字符出现的次数进行编码，按出现次数编码，出现次数越多的，则编码越小：

    比如空格出现最多次，然后是a，以此类推......

    1
    0=  ，1=a，10=i，11=o......

    当传输的信息越多的时候，变长编码实际传输的长度相对定长编码就越小

另外，我们还需要了解一下什么是补码：

计算机里面只有加法器，没有减法器，所以减法必须用加法来完成。 对于 100 以内的十进制数，“-1”就可以用"+99"代替。比如 25 － 1 ＝ 24，可以写成 25 ＋ 99 ＝ (1)24。 如果限定了两位数，那“-1”和“+99”就是等效的。同样，“-2”可以用“+98”代替。

它们之间，称为补数，而100就称为模。

对于8位二进制数：0000 0000~1111 1111(255)，模为256。 －1，可以用 +255(1111 1111)代替。 －2，可以用 +254(1111 1110)代替

这些二进制数，就称为负数的补码

二、赫夫曼编码思路

同样举个例子，我们要传输 i like like like java do you like a java这段话

  1. 统计各字符的出现次数

    1
    d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9

  2. 将字符出现次数作为节点的权，构建一个赫夫曼树（这里步骤同上一篇文章）

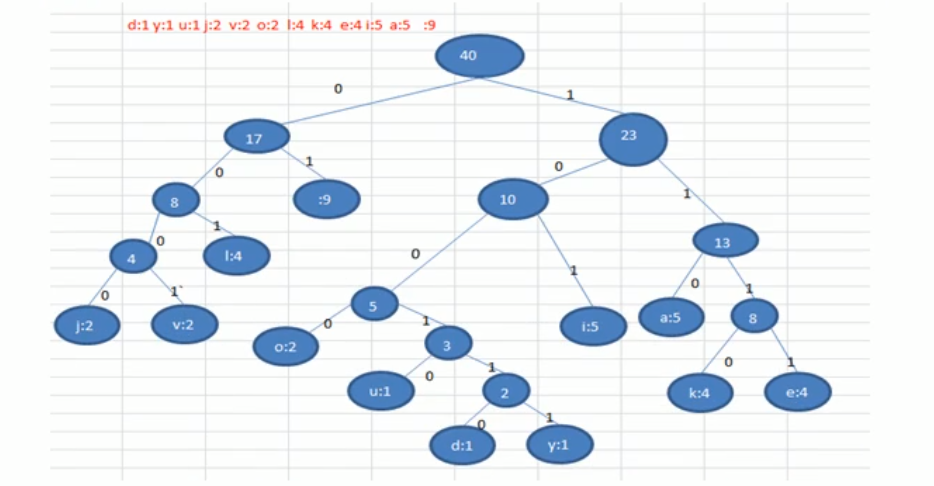
    image-20200717213740072

  3. 我们使用0和1来描述某个节点在树中往左或往右的路径，比如j，从根节点出发抵达j的路径就是0000，抵达i的路径就是101

    于是现在对所有字符的路径进行统计，就有：

    1
    2
    o: 1000     u: 10010     d: 100110     y: 100111    i: 101    a : 110
    k: 1110     e: 1111      j: 0000       v: 0001      l: 001      : 01

  4. 按照上面的路径，我们将其转为二进制

    1
    1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110

    直接转为二进制长度为359，而经过赫夫曼编码长度则是133，与直接转为二进制相比，缩短了62.9%

三、代码实现

1.创建节点类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * @Author：CreateSequence
 * @Date：2020-07-18 13:28
 * @Description：赫夫曼编码用节点
 */
public class HuffmanCodeNode implements Comparable<HuffmanCodeNode>{

    //字符
    Byte data;
    //权值
    int weight;
    HuffmanCodeNode left;
    HuffmanCodeNode right;

    public HuffmanCodeNode(Byte data, int weight) {
        this.data = data;
        this.weight = weight;
    }

    public HuffmanCodeNode(HuffmanCodeNode left, HuffmanCodeNode right) {
        //计算子节点权值之和
        this.weight = left.weight + right.weight;
        this.left = left;
        this.right = right;
    }

    @Override
    public int compareTo(HuffmanCodeNode o) {
        //从小到大排序
        return this.weight - o.weight;
    }

    @Override
    public String toString() {
        return "{" +
            "data=" + data +
            ", weight=" + weight +
            '}';
    }
    
}

2.统计字符出现次数，并组装节点列表

对应思路中的第一步：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * 统计字符在字符串中的出现次数，并组装节点列表
 * @param str 字符串
 * @return
 */
private List<HuffmanCodeNode> getNodes(String str) {
    //将字符串转为字符串数组
    byte[] strBytes = str.getBytes();

    //遍历字节数组，并且统计某一字符出现次数
    Map<Byte, Integer> counts = new HashMap<>(24);
    for (byte b : bytes) {
        Integer count = counts.get(b);
        //判断某一字符是否第一次出现
        if (count == null) {
            counts.put(b, 1);
        }else {
            //不是就让出现次数+1
            counts.put(b, count ++);
        }
    }

    //将map转为节点集合
    List<HuffmanCodeNode> nodes = new ArrayList<>();
    for (Map.Entry<Byte, Integer> entry : counts.entrySet()) {
        nodes.add(new HuffmanCodeNode(entry.getKey(), entry.getValue()));
    }

    return nodes;
}

3.生成赫夫曼树

对应思路中的第二步：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * 构建赫夫曼树
 * @param nodes 节点集合
 * @return 最终生成的树的根节点
 */
private HuffmanCodeNode createTree(List<HuffmanCodeNode> nodes) {
    //构建树
    while (nodes.size() > 1) {
        //从小到大排序
        Collections.sort(nodes);
        //取出最小的两个数构建树
        HuffmanCodeNode left = nodes.get(0);
        HuffmanCodeNode right = nodes.get(1);
        HuffmanCodeNode parant = new HuffmanCodeNode(left, right);
        //删除两个节点
        nodes.remove(left);
        nodes.remove(right);
        //将根节点添加至集合
        nodes.add(parant);
    }
    //返回树的根节点
    return nodes.get(0);
}

当然，这个时候可以通过前序遍历来检查是否构建成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * 前序遍历
 * @param node 树的根节点
 */
private void preOrder(HuffmanCodeNode node) {
    //递归
    System.out.println(node.toString());
    if (node.left != null) {
        preOrder(node.left);
    }
    if (node.right != null) {
        preOrder(node.right);
    }
}

4.得到赫夫曼编码

对应思路中的第三步：

我们已经得到了赫夫曼树，现在我们需要获得从根节点到各个叶子结点的路径，也就是赫夫曼编码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * 生成赫夫曼树对应的赫夫曼编码集合
 */
private Map<Byte, String> huffmanCodes = new HashMap<>();
/**
 * 储存某个叶子节点的拼接路径
 */
private StringBuilder stringBuilder = new StringBuilder();

/**
 * 将传入的节点作为树的根节点，找到其所有的叶子结点的赫夫曼编码，并放入赫夫曼编码集合
 * @param node 节点
 * @param way 叶子结点的路径，左为0，右为1
 * @param builder 用于拼接路径
 */
private Map<Byte, String> getCodes(HuffmanCodeNode node, String way, StringBuilder builder) {
    StringBuilder stringBuilder = new StringBuilder(builder);
    //建路径拼接至上一路径
    stringBuilder.append(way);
    if (node != null) {
        //判断当前是否为叶子节点
        if (node.data == null) {
            //向左右递归直到找到叶子结点
            getCodes(node.left, "0", stringBuilder);
            getCodes(node.right, "1", stringBuilder);
        }else {
            //已经是叶子结点，将路径存入集合
            huffmanCodes.put(node.data, stringBuilder.toString());
        }
    }
    return huffmanCodes;
}

public Map<Byte, String> getCodes() {
    //构建赫夫曼树
    HuffmanCodeNode root = createTree();
    //处理左右子树
    getCodes(root.left, "0", stringBuilder);
    getCodes(root.right, "1", stringBuilder);
    //返回赫夫曼编码
    return huffmanCodes;
}

5.将得到的赫夫曼编码转回字节数组

对应思路中的第四步，也就是最后一步：

我们得到了赫夫曼编码表，也就是这玩意： Map<Byte, String> huffmanCodes，每串赫夫曼编码字符串都对应一个字符，我们需要处理赫夫曼编码的每一个字符，将其转为二进制后再转为byte，最后处理完得到一队字节数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
 * 将字符串对应的byte数组，转换为经过赫夫曼编码压缩后的byte数组
 * @param bytes
 * @param huffmanCodes
 * @return
 */
private byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
    //获取赫夫曼编码
    StringBuilder stringBuilder = new StringBuilder();
    //遍历byte数组，一个byte表示一个字符
    for (Byte b : bytes) {
        //将字符转为赫夫曼编码格式，一个字符对应8位编码
        stringBuilder.append(huffmanCodes.get(b));
    }

    //一个字符对应对应的8位的赫夫曼编码，如果赫夫曼编码无法被8整除，就直接补齐赫夫曼编码不足八位的那一个字符
    int len = stringBuilder.length() % 8 == 0 ? stringBuilder.length() / 8 : stringBuilder.length() / 8 + 1;
    //System.out.println("有几个字符："+len);

    //将压缩后的赫夫曼编码按字符分开存储
    byte[] huffmanCodeBytes = new byte[len];
    //计录已处理几个字符
    int index = 0;
    //每8位编码对应一个byte，所以步长为8
    //每循环一次处理一个byte，也就是一个字符
    for (int i = 0; i < stringBuilder.length(); i += 8) {
        String strBytes;
        //判断编码长度是否超过8位
        if (i + 8 < stringBuilder.length()) {
            //超过8位就从赫夫曼编码截取八位（也就是一个字符）
            strBytes = stringBuilder.substring(i, i + 8);
        }else {
            //否则就有多少截多少
            strBytes = stringBuilder.substring(i);
        }
        //将赫夫曼编码转为二进制，存入byte数组
        huffmanCodeBytes[index] = (byte) Integer.parseInt(strBytes, 2);

        //位已处理字符数+1
        index++;
    }

    //循环结束后，返回赫夫曼编码按字符转换得到的字节数组
    return huffmanCodeBytes;
}

public byte[] zip() {
    byte[] bytes = str.getBytes();
    Map<Byte, String> huffmanCodes = getCodes();
    return zip(bytes, huffmanCodes);
}

6.解码

信息被赫夫曼编码处理后我们会得到一队字节数组，如果要解码，我们需要先把字节数组按字符一个字节一个字节的转为二进制，然后通过赫夫曼编码表把二进制和字符字节一一找出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
/**
 * 将byte转成二进制字符串
 * @param isComple 是否需要补高位。最后一个字节无需补位
 * @param b 要转换的字节
 * @return
 */
private String byteToString(boolean isComplate, byte b) {
    int temp = b;
    //判断是否需要补齐高位
    if (isComplate) {
        temp |= 256;
    }
    //返回temp对应的二进制补码
    String str = Integer.toBinaryString(temp);
    return isComplate ? str.substring(str.length() - 8) : str;
}

/**
 * 解码
 * @param huffmanCodes 赫夫曼编码表
 * @param huffmanBytes 赫夫曼编码处理过的字节数组
 * @return 原来未被转为赫夫曼编码的的字符串字节素组
 */
private byte[] decode(Map<Byte, String> huffmanCodes, byte[] huffmanBytes) {

    //将赫夫曼编码处理过byte数组转为二进制字符串
    StringBuilder stringBuilder = new StringBuilder();
    for (int i = 0; i < huffmanBytes.length; i++) {

        boolean isComplate = true;
        //如果是最后一个字节就不用补高位了
        if (i == huffmanBytes.length - 1) {
            isComplate = false;
        }
        //拼接字节转的二进制字符串
        stringBuilder.append(byteToString(isComplate, huffmanBytes[i]));
    }

    //把字符串按照指定赫夫曼编码进行解码
    //原本赫夫曼编码表是<字节，二进制字符串>，现在要转为<二进制字符串，字节>以通过转换得到的二进制字符串取出对应的字节
    Map<String, Byte> reHuffmanCodes = new HashMap<>();
    for (Map.Entry<Byte, String> entry : huffmanCodes.entrySet()) {
        reHuffmanCodes.put(entry.getValue(), entry.getKey());
    }

    List<Byte> bytes = new ArrayList<>();
    //由于无法确认拼接后的二进制字符串每八位一定就能和某个字节对应，所以需要进行字符串匹配
    //这里可以简单理解为双指针，一号指针从i开始，二号指针从i+1开始
    //一号指针先指向字符串第i字符，然后二号指针从i+1个字符开始不断后移，然后进行进行匹配
    //比如：i=0，j=1，第一次截取并匹配的字符就是[0,1),也就是0；第二次是[0,2)，也就是01；然后是[0,3).....以此类推
    //直到找到以后，比如[2,7)，就移动一号指针到7，二号指针移动到8
    for (int i = 0, j = 1; i < stringBuilder.length(); i = --j) {
        String key = "";
        while (!reHuffmanCodes.containsKey(key)) {
            key = stringBuilder.substring(i, j);
            j++;
        }
        bytes.add(reHuffmanCodes.get(key));
    }

    //由集合转为字节数组
    byte b[] = new byte[bytes.size()];
    for (int i = 0; i < b.length; i++) {
        b[i] = bytes.get(i);
    }

    return b;
}

四、完整代码

具体代码和测试用例可以去GitHub上看，这里就放实现类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
import java.util.*;

/**
 * @Author：CreateSequence
 * @Date：2020-07-18 13:26
 * @Description：赫夫曼编码
 */
public class HuffmanCode {

    private String str;

    public String getStr() {
        return str;
    }

    public HuffmanCode(String code) {
        if (code.length() == 0 || code == null) {
            throw new RuntimeException("字符串必须有至少一个字符！");
        }
        this.str = code;
    }

    /**
     * 统计字符在字符串中的出现次数，并组装节点列表
     * @return
     */
    public List<HuffmanCodeNode> getNodes() {
        //将字符串转为字符串数组
        byte[] bytes = str.getBytes();

        //遍历字节数组，并且统计某一字符出现次数
        Map<Byte, Integer> counts = new HashMap<>(24);
        for (byte b : bytes) {
            Integer count = counts.get(b);
            //判断某一字符是否第一次出现
            if (count == null) {
                counts.put(b, 1);
            }else {
                //不是就让出现次数+1
                counts.put(b, count ++);
            }
        }

        //将map转为节点集合
        List<HuffmanCodeNode> nodes = new ArrayList<>();
        for (Map.Entry<Byte, Integer> entry : counts.entrySet()) {
            nodes.add(new HuffmanCodeNode(entry.getKey(), entry.getValue()));
        }

        return nodes;
    }

    /**
     * 构建赫夫曼树
     * @param nodes
     * @return
     */
    private HuffmanCodeNode createTree(List<HuffmanCodeNode> nodes) {
        //构建树
        while (nodes.size() > 1) {
            //从小到大排序
            Collections.sort(nodes);
            //取出最小的两个数构建树
            HuffmanCodeNode left = nodes.get(0);
            HuffmanCodeNode right = nodes.get(1);
            HuffmanCodeNode parant = new HuffmanCodeNode(left, right);
            //删除两个节点
            nodes.remove(left);
            nodes.remove(right);
            //将根节点添加至集合
            nodes.add(parant);
        }
        //返回树的根节点
        return nodes.get(0);
    }
    public HuffmanCodeNode createTree(){
        return createTree(getNodes());
    }

    /**
     * 前序遍历
     * @param node 树的根节点
     */
    private void preOrder(HuffmanCodeNode node) {
        //递归
        System.out.println(node.toString());
        if (node.left != null) {
            preOrder(node.left);
        }
        if (node.right != null) {
            preOrder(node.right);
        }
    }
    public void preOrder(){
        HuffmanCodeNode root = createTree(getNodes());
        preOrder(root);
    }

    /**
     * 生成赫夫曼树对应的赫夫曼编码集合
     */
    private Map<Byte, String> huffmanCodes = new HashMap<>();
    /**
     * 储存某个叶子节点的拼接路径
     */
    private StringBuilder stringBuilder = new StringBuilder();

    /**
     * 将传入的节点作为树的根节点，找到其所有的叶子结点的赫夫曼编码，并放入赫夫曼编码集合
     * @param node 节点
     * @param way 叶子结点的路径，左为0，右为1
     * @param builder 用于拼接路径
     */
    private Map<Byte, String> getCodes(HuffmanCodeNode node, String way, StringBuilder builder) {
        StringBuilder stringBuilder = new StringBuilder(builder);
        //建路径拼接至上一路径
        stringBuilder.append(way);
        if (node != null) {
            //判断当前是否为叶子节点
            if (node.data == null) {
                //向左右递归直到找到叶子结点
                getCodes(node.left, "0", stringBuilder);
                getCodes(node.right, "1", stringBuilder);
            }else {
                //已经是叶子结点，将路径存入集合
                huffmanCodes.put(node.data, stringBuilder.toString());
            }
        }
        //返回赫夫曼编码
        return huffmanCodes;
    }

    public Map<Byte, String> getCodes() {
        //构建赫夫曼树
        HuffmanCodeNode root = createTree();
        //处理左右子树
        getCodes(root.left, "0", stringBuilder);
        getCodes(root.right, "1", stringBuilder);
        //返回赫夫曼编码
        return huffmanCodes;
    }

    /**
     * 将字符串对应的byte数组，转换为经过赫夫曼编码压缩后的byte数组
     * @param bytes
     * @param huffmanCodes
     * @return
     */
    private byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
        //获取赫夫曼编码
        StringBuilder stringBuilder = new StringBuilder();
        //遍历byte数组，一个byte表示一个字符
        for (Byte b : bytes) {
            //将字符转为赫夫曼编码格式，一个字符对应8位编码
            stringBuilder.append(huffmanCodes.get(b));
        }

        //一个字符对应对应的8位的赫夫曼编码，如果赫夫曼编码无法被8整除，就直接补齐赫夫曼编码不足八位的那一个字符
        int len = stringBuilder.length() % 8 == 0 ? stringBuilder.length() / 8 : stringBuilder.length() / 8 + 1;
        //System.out.println("有几个字符："+len);

        //将压缩后的赫夫曼编码按字符分开存储
        byte[] huffmanCodeBytes = new byte[len];
        //计录已处理几个字符
        int index = 0;
        //每8位编码对应一个byte，所以步长为8
        //每循环一次处理一个byte，也就是一个字符
        for (int i = 0; i < stringBuilder.length(); i += 8) {
            String strBytes;
            //判断编码长度是否超过8位
            if (i + 8 < stringBuilder.length()) {
                //超过8位就从赫夫曼编码截取八位（也就是一个字符）
                strBytes = stringBuilder.substring(i, i + 8);
            }else {
                //否则就有多少截多少
                strBytes = stringBuilder.substring(i);
            }
            //将赫夫曼编码转为二进制，存入byte数组
            huffmanCodeBytes[index] = (byte) Integer.parseInt(strBytes, 2);

            //位已处理字符数+1
            index++;
        }

        //循环结束后，返回赫夫曼编码按字符转换得到的字节数组
        return huffmanCodeBytes;
    }
    public byte[] zip() {
        byte[] bytes = str.getBytes();
        Map<Byte, String> huffmanCodes = getCodes();
        return zip(bytes, huffmanCodes);
    }

    /**
     * 将byte转成二进制字符串
     * @param isComple 是否需要补高位。最后一个字节无需补位
     * @param b 要转换的字节
     * @return
     */
    private String byteToString(boolean isComplate, byte b) {
        int temp = b;
        //判断是否需要补齐高位
        if (isComplate) {
            temp |= 256;
        }
        //返回temp对应的二进制补码
        String str = Integer.toBinaryString(temp);
        return isComplate ? str.substring(str.length() - 8) : str;
    }

    /**
     * 解码
     * @param huffmanCodes 赫夫曼编码表
     * @param huffmanBytes 赫夫曼编码处理过的字节数组
     * @return 原来未被转为赫夫曼编码的的字符串字节素组
     */
    private byte[] decode(Map<Byte, String> huffmanCodes, byte[] huffmanBytes) {

        //将赫夫曼编码处理过byte数组转为二进制字符串
        StringBuilder stringBuilder = new StringBuilder();
        for (int i = 0; i < huffmanBytes.length; i++) {

            boolean isComplate = true;
            //如果是最后一个字节就不用补高位了
            if (i == huffmanBytes.length - 1) {
                isComplate = false;
            }
            //拼接字节转的二进制字符串
            stringBuilder.append(byteToString(isComplate, huffmanBytes[i]));
        }

        //把字符串按照指定赫夫曼编码进行解码
        //原本赫夫曼编码表是<字节，二进制字符串>，现在要转为<二进制字符串，字节>以通过转换得到的二进制字符串取出对应的字节
        Map<String, Byte> reHuffmanCodes = new HashMap<>();
        for (Map.Entry<Byte, String> entry : huffmanCodes.entrySet()) {
            reHuffmanCodes.put(entry.getValue(), entry.getKey());
        }

        List<Byte> bytes = new ArrayList<>();
        //由于无法确认拼接后的二进制字符串每八位一定就能和某个字节对应，所以需要进行字符串匹配
        //这里可以简单理解为双指针，一号指针从i开始，二号指针从i+1开始
        //一号指针先指向字符串第i字符，然后二号指针从i+1个字符开始不断后移，然后进行进行匹配
        //比如：i=0，j=1，第一次截取并匹配的字符就是[0,1),也就是0；第二次是[0,2)，也就是01；然后是[0,3).....以此类推
        //直到找到以后，比如[2,7)，就移动一号指针到7，二号指针移动到8
        for (int i = 0, j = 1; i < stringBuilder.length(); i = --j) {
            String key = "";
            while (!reHuffmanCodes.containsKey(key)) {
                key = stringBuilder.substring(i, j);
                j++;
            }
            bytes.add(reHuffmanCodes.get(key));
        }

        //由集合转为字节数组
        byte b[] = new byte[bytes.size()];
        for (int i = 0; i < b.length; i++) {
            b[i] = bytes.get(i);
        }

        return b;
    }

    public byte[] decode(byte[] huffmanBytes) {
        return decode(huffmanCodes, huffmanBytes);
    }

}
0%