发表于 | 分类于
字数统计: 1.7k

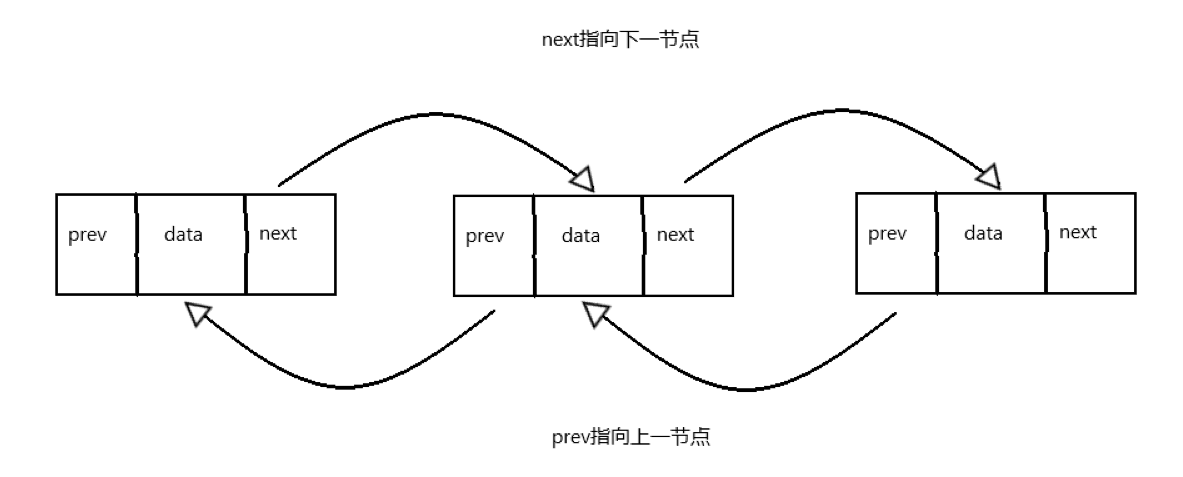
概述

衡量一个算法的好坏，最简单的标准就是他的时间复杂度。

算法的时间复杂度（Time complexity）是一个函数，它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。

时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，亦即考察输入值大小趋近无穷时的情况。

例如，如果一个算法对于任何大小为 n （必须比 n0 大）的输入，它至多需要 5n3 + 3n 的时间运行完毕，那么它的渐近时间复杂度是 O(n3).

一、时间频度

要理解时间复杂度，需要先理解时间频度，而时间频度简单的说，就是算法中语句的执行次数。

举个例子：

要计算1+2+...+100，现在有两种算法

1
2
3
4
5
6
7
8
9
10
11
12
public int fun1(int n){
    int total;
    for(int i = 0; i <= n; i++){
        total+=i;
    }
    return total;
}

public int fun2(int n){
    int total = (1 + n)*n/2;
    return total;
}

我们可以看见，对于fun1()这个方法，不管n多大，永远需要执行n+1次，也就是说他的时间频度是T(n)=n+1,

而对与fun2()来说，不管n多大都只需要执行1次，所以他的时间频度T(n)=1。

阅读全文 »

发表于 | 分类于
字数统计: 1.1k

概述

最近接触了 java 并发编程，其中接触到了挺多的新名词：进程，线程，并行，并发，同步，异步，阻塞，非阻塞。其中大部分是其实是操作系统的概念，在这里先简单的提前了解一下，做一下区分。算是为操作系统做个预习。

一、串行，并行，并发

1.名称解释

  • 串行：程序按顺序执行，同一时间只能执行一个程序，前一个执行完毕后才轮到后一个

  • 并行：多个程序可以同时执行，宏观和微观上看程序都是同时执行

  • 并发：同一时刻只有一条程序执行，但是多个进程被快速轮换执行，宏观上看是同时执行，微观上看只是把时间分成若干段，使多个进程快速交替的执行

并发与并行关注的是程序是否在同一时间内同时被执行

2.举个例子

  • 串行：你吃饭吃到一半，电话来了，你一直到吃完了以后才去接
  • 并发：你吃饭吃到一半，电话来了，你接了电话聊了两句，停下来吃了两口饭，又拿起电话聊了两句
  • 并行：你吃饭吃到一半，电话来了，你一边打电话一边吃饭

另外：

阅读全文 »

发表于 | 分类于
字数统计: 1.9k

一、迷宫回溯问题

1.问题

一个7*8的数组模拟迷宫，障碍用1表示，通路使用0表示，给定起点（1,1）和终点（6,5），要求给出起点到终点的通路

2.解题思路

  1. 首先，我们需要给程序一个寻向的基本策略，我们先假定寻向顺序为“下-右-上-左”，也就是说从起点出发，先往下走，往下走不通就往右.....以此类推
  2. 然后我们需要给走过的路一个标记，暂记为2
  3. 而当从一个方向走到一个只能原路返回的死胡同时，就给这段路标记为3
  4. 当抵达终点坐标（6,5）时程序结束

3.代码实现

3.1生成地图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * 创建一个二维数组,用于模拟8*7迷宫
 * 使用1表示不可通过的实心方块，0表示可通过砖块
 * （6,5）为默认终点，（1,1）为默认起点
 * @return
 */
public static int[][] getMap(){
    int[][] map = new int[8][7];
    //上下全置为1
    for(int i = 0;i <7 ;i++){
        map[0][i] = 1;
        map[7][i] = 1;
    }
    //左右全置为1
    for(int i = 0;i < 8;i++){
        map[i][0] = 1;
        map[i][6] = 1;
    }
    //设置挡板
    map[3][1] = 1;
    map[3][2] = 1;

    //输出地图
    System.out.println("地图的初始情况:");
    showMap(map);

    return map;
}

/**
 * 展示地图
 * @param map
 */
public static void showMap(int[][] map) {
    for(int i = 0;i < 8;i++){
        for(int j = 0;j < 7;j++){
            System.out.print(map[i][j] + " ");
        }
        System.out.println();
    }
}

3.2 寻路逻辑的实现

阅读全文 »

发表于 | 分类于
字数统计: 738

一、什么是递归

所谓递归，简单点来说，就是一个函数直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。

引用知乎大佬的例子：

我们可以把” 递归 “比喻成 “查字典 “，当你查一个词，发现这个词的解释中某个词仍然不懂，于是你开始查这第二个词。

可惜，第二个词里仍然有不懂的词，于是查第三个词，这样查下去，直到有一个词的解释是你完全能看懂的，那么递归走到了尽头，然后你开始后退，逐个明白之前查过的每一个词，最终，你明白了最开始那个词的意思。

我们把查字典理解成一个函数search(){}，而“明白了”就是停止条件。

按这个思路，那这个流程就是这样的：

1
2
3
4
5
6
7
8
public void search(){
    //如果明白了就停止函数
    if("明白了"){
       return;
    }
    //没明白调用自己继续查
    search();
}

我们举个简单的例子：

要计算阶乘1*2*3*.....*(n-1)*n，代码如下：

1
2
3
4
5
6
7
8
public static int mult(int n) {
    //终止条件，当n=1时直接返回1
    if (n == 1){
        return n;
    }
    //计算n*(n-1).....
    return n * mult(n - 1);
}
阅读全文 »

发表于 | 分类于
字数统计: 2.6k

一、计算器的计算思路分析

我们以计算3+8*2-6这个算式为例：

  1. 将算式解析为数字和符号：3，+，8，*，2，-，6

  2. 准备一个用于存放数字的数字栈numStack，还有一个存放运算符号的符号栈symbolStack，下面分别简称栈n和栈s

  3. 按顺序扫描解析后的数字和符号，

    如果是数字，就直接入数栈n，

    如果是符号，且如果符号栈s为空，就直接入栈，

    如果s不为空，就需要比较栈顶符号与当前符号的优先级，再分两种情况：

    • 如果栈顶符号优先级比当前符号大，就从栈n弹出两个数字，从栈s弹出一个符号，然后进行运算，最后得出的结果再入栈n
    • 如果栈顶符号优先级小于或等于当前符号，就将符号入栈s

按照这个流程，扫描完后栈n会留下3，16，6这三个数，栈s会留下+，-这两个 符号，

然后按顺序，栈n弹出两个数字，栈s弹出一个符号，然后运算得到结果后再入栈n，重复此步骤，最后栈s清空，栈n只剩一个数字，即为运算结果。

二、代码实现

我们先来实现一个加减乘除的数计算器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
/**
 * @Author：黄成兴
 * @Date：2020-06-25 16:29
 * @Description：使用栈实现一个计算器
 */
public class StackCalculator {

    //数字栈
    public Stack<Integer> numStack = new Stack<>();

    //符号栈
    public Stack<String> symbolStack = new Stack<>();

    /**
     * 根据计算公式运算并输出结果
     * @param expression 计算公式
     */
    public void calculate(String expression) {
        //用于多位数拼接
        String numStr = "";

        //遍历字符串里的每一个字符
        for (int i = 0; i < expression.length() ; i++) {
            String ch = expression.substring(i, i + 1);
            
            //检验是否数字
            if (ch.matches("[0-9]")) {
                //如果该数字已经是最后一个字符就直接存入数字栈
                if (i == expression.length() - 1){
                    numStack.push(Integer.valueOf(ch));
                }else {
                    //如果不是字符串最后一个字符，就拼接入字符串
                    numStr += ch;
                }
                continue;
            }
            //如果是符号，就把之前拼接的多位数存入数字栈
            numStack.push(Integer.valueOf(numStr));
            numStr = "";
            
            //如果是符号就比较符号优先级
            if (isFrist(ch)){
                //如果当前符号与符号栈栈栈顶符号优先或者平级就入栈
                symbolStack.push(ch);
            }else {
                //否则就从栈中取两数字和一个符号先计算
                int num = getCalculateResult();
                //再把计算结果入数栈
                numStack.push(num);
                //再把当前符号入栈
                symbolStack.push(ch);
            }
        }

        //当符号栈为空时，说明计算完成，此时数字栈唯一数字即为结果
        while (!symbolStack.empty()) {
            int result = getCalculateResult();
            numStack.push(result);
        }
        System.out.println("计算结束！结果为：" + numStack.pop());
    }
    
    /**
     * 根据数字和符号运算并返回结果
     * @param num1 后出栈的数字
     * @param num2 先出栈的数字
     * @param symbol 运算符号
     * @return
     */
    public int getCalculateResult(int num1, int num2, String symbol) {
        int result = 0;
        //根据符号进行运算
        switch (symbol){
            case "+":
                result = num1 + num2;
                break;
            case "-":
                result = num1 - num2;
                break;
            case "*":
                result = num1 * num2;
                break;
            case "/":
                result = num1 / num2;
                break;
                default:
                    throw new RuntimeException("只支持加减乘除运算！");
        }

        System.out.println(num1 + symbol + num2 + "=" + result);

        return result;
    }

    /**
     * 直接从数栈取两数字，符号栈取一符号进行计算
     * @return
     */
    public int getCalculateResult() {
        int num1 = numStack.pop();
        int num2 = numStack.pop();
        String symbol = symbolStack.pop();
        int result = getCalculateResult(num2, num1, symbol);
        return result;
    }

    /**
     * 比较符号和当前符号栈顶符号的优先级。
     * 如果当前符号优先级小于符号栈栈顶符号的优先级，就返回false，否则返回true
     * 如果当前符号栈为空，直接返回true
     * @param symbol
     * @return
     */
    public boolean isFrist(String symbol) {
        //判断当前符号栈是否为空
        if (symbolStack.empty()) {
            return true;
        }
        //取出并放回栈顶符号
        String stackSymbol = symbolStack.pop();
        symbolStack.push(stackSymbol);

        //栈顶符号的优先级
        int stackSymbolGrade = getSymbolGrade(stackSymbol);
        //当前符号的优先级
        int symbolgrade = getSymbolGrade(symbol);

        return symbolgrade > stackSymbolGrade;
    }

    /**
     * 根据符号返回符号的优先级
     * @param symbol
     * @return 加减返回0，乘除返回1
     */
    public int getSymbolGrade(String symbol) {
        int grade;
        if ("+".equals(symbol) || "-".equals(symbol)) {
            grade = 0;
        } else if ("*".equals(symbol) || "/".equals(symbol)) {
            grade = 1;
        }else {
            throw new RuntimeException("不支持的操作符类型：" + symbol);
        }
        return grade;
    }
}

现在输入运算公式调用calculate()函数即可得出结果，但是目前这个计算器仍然还有致命问题没有解决：

阅读全文 »

发表于 | 分类于
字数统计: 807

一、什么是栈

栈（stack）是一种先进后出的有序列表，其中的元素只能在线性表的同一端进出，

允许元素插入和删除的一端被称为栈顶（top），固定的另一端被称为栈底（button）。

二、数组简单实现栈

由于栈是只在一端进出，也就是说相比队列实际上只需要有一个栈顶指针top即可：

  1. 当栈空时top为-1
  2. 入栈后top+1
  3. 出栈后top-1

根据思路我们可以用数组实现一个简单的栈：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
/**
 * @Author：huang
 * @Date：2020-06-23 16:51
 * @Description：使用数组模拟栈
 */
public class Stack {

    private int maxSize;
    private int top = -1;
    private Object[] arr;

    public Stack(int maxSize) {
        this.maxSize = maxSize;
        this.arr = new Object[maxSize];
    }

    /**
     * 判断栈满
     * @return
     */
    public boolean isFull() {
        return top == maxSize - 1;
    }

    /**
     * 判断栈空
     * @return
     */
    public boolean isEmpty() {
        return top == -1;
    }

    /**
     * 入栈
     * @param item
     */
    public void push(Object item) {
        //判断栈是否已满
        if (isFull()) {
            throw new RuntimeException("栈已满");
        }
        //入栈
        top = top + 1;
        arr[top] = item;
    }

    /**
     * 出栈
     */
    public Object pop() {
        if (isEmpty()) {
            throw new RuntimeException("栈为空！");
        }
        Object item = arr[top];
        top--;
        return item;
    }

    /**
     * 遍历栈
     */
    public void show() {
        if (isEmpty()) {
            throw new RuntimeException("栈为空！");
        }
        //遍历并打印栈中元素
        for (int i = top; i >= 0; i--) {
            System.out.println("stack" + i + "：" + arr[i]);
        }
    }
}

三、链表简单模拟栈

阅读全文 »

发表于 | 分类于
字数统计: 1.3k

一、双向链表

双向链表与单链表基本相似，但是最大的区别在于双向链表在节点中除了指向下一节点的next指针外，还有指向前一节点的prev指针，这使得双向链表在可以在任意节点从头尾两个方向进行遍历，是“双向”的。

和单链表相比，双向链表在删除和查询等方面明显在操作上更具有灵活性，但是会消耗更多的内存，需要根据使用条件进行取舍。

java中的LinkedHashMap的本质即是一个双向链表。

二、双向链表的简单实现

修改原来的Node类，在里面添加一个新成员变量Node prev

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * @Author：huang
 * @Date：2020-06-20 10:19
 * @Description：节点类
 */
public class Node {

    //节点序号
    int num;

    //数据
    Object data;

    //下一个节点
    Node next;

    //上一节点
    Node prev;

    public Node(int num, Object data) {
        this.num = num;
        this.data = data;
    }

    @Override
    public String toString() {
        return "Node{" +
            "num=" + num +
            ", data=" + data +
            '}';
    }
}

1.添加

添加与单向链表代码逻辑一样，但是新节点在添加时需要修改prev指针指向原来的尾节点。

阅读全文 »

发表于 | 分类于
字数统计: 2.3k

一、什么是链表

链表是一种数据结构，跟数组不同，链表不需要连续的内存空间，而是通过指针将零散的内存块连接起来。

因此，链表的查找需要通过节点按顺序遍历，而增加与删除通过只需要操作指针指向，这也造成了相比数组，链表的查找性能消耗大而增加和删除消耗小的特点。

链表由节点组成，一般每个节点最少包含用于储存数据的data区和用于指向下一个节点的指针next，有的链表可能会有头结点或尾结点用于存储链表长度等信息。

二、链表的简单实现

先来实现一个简单的节点类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * @Author：huang
 * @Date：2020-06-20 10:19
 * @Description：节点类
 */
public class Node {

    //节点序号
    int num;

    //数据
    Object data;

    //下一个节点
    Node next;

    public Node(int num, Object data) {
        this.num = num;
        this.data = data;
    }
    
    public int getNum() {
        return num;
    }

    public Object getData() {
        return data;
    }

    public void setNum(int num) {
        this.num = num;
    }

    public void setData(Object data) {
        this.data = data;
    }
    
    @Override
    public String toString() {
        return "Node{" +
            "num=" + num +
            ", data=" + data +
            '}';
    }
}

1.插入节点

1.1不按照排序的插入

阅读全文 »

发表于 | 分类于
字数统计: 1.4k

一、什么是队列

队列是一种特殊的线性表。

队列元素的进出遵循“先进先出”原则：即只允许在前端（front）也就是队头进行删除操作，而只能在后端（rear）也就是队尾进行插入操作。

如图所示：

  • 队列的最大长度为MaxSize，最大下标为MaxSize-1
  • 入队时队头下标不变而队尾下标改变，出队时则相反

二、模拟队列

1.简单的使用数组模拟队列：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
/**
 * @Author：huang
 * @Date：2020-06-11 16:28
 * @Description：用数组模拟队列
 */
public class Queue {

    //队列最大长度
    private int maxSize;
    //存放数据的数组
    private Object[] arr;
    //头指针，指向队头的元素的前一个位置
    private int front;
    //尾指针，指向队尾的元素所在位置
    private int rear;

    //构造器
    public Queue(int size) {
        this.maxSize = size;
        this.arr = new Object[maxSize];
        this.front = -1;
        this.rear = -1;
    }

    /**
     * 判断队列是否为空
     *
     * @return
     */
    public boolean isEmpty() {
        //当头指针和尾指针相等时队列为空
        return rear == front;
    }

    /**
     * 判断队列是否已满
     * @return
     */
    public boolean isFull(){
        //当尾指针等于maxSize-1时队列满
        return rear == maxSize - 1;
    }

    /**
     * 入队
     * @param item 入队元素
     * @return
     */
    public int addQueue(Object item) {
        //判断队列是否已满
        if (isFull()) {
            throw new RuntimeException("队列已满！");
        }
        //尾指针后移
        rear++;
        arr[rear] = item;
        return rear;
    }

    /**
     * 出队
     * @return
     */
    public Object quitQueue() {
        //判断队列是否为空
        if (isEmpty()) {
            throw new RuntimeException("队列为空！");
        }
        //头指针后移
        front++;
        return arr[front];
    }

}

2.解决“内存溢出”

阅读全文 »

发表于 | 分类于
字数统计: 1.3k

概述

最早之前博客一直是用有道云笔记写的，后面接触了 markdown 后改用 Typora 方便了不少，但是上传的时候图片仍然还要另外上传，着实麻烦。于是决定用七牛云自己搭一个图床。

一、创建并上传文件到存储空间

1.注册七牛账号，并且实名认证

2.创建储存空间

打开侧边栏，选择对象存储

选择新建空间

  • 存储空间名称：按规则随便取
  • 存储区域：选择离靠近的地区
  • 访问控制：选择公开，否则外网无法访问，没法作为图床
阅读全文 »
0%