数据结构与算法（十三）：赫夫曼树

发表于 | 分类于
字数统计: 742

一、什么是赫夫曼树

给定n个权值作为n个叶子节点，构造一课二叉树，若该树的带权路径长度和（wpl）达到最小，称这样的二叉树为最优二叉树，也就是赫夫曼树。

要理解这句话，我们需要了解几个关键词：

  • 路径：从一个节点往下一个节点之间的通路。若根节点层数为1，则根节点通往L层的节点路径长度为L-1
  • 带权路径：权可以理解为节点值，而从根节点到某节点之间的路径长度与该点的权的成绩称为带权路径长度

举个例子：

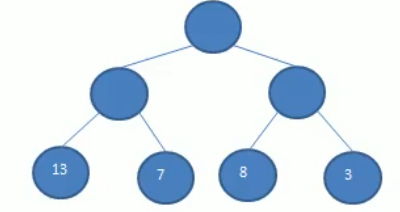
image-20200717165237484

如上图所示，节点13到根节点的路径长度是2，而权是13，所以带权路径长度就是2*13=26，同理，节点7的带权路径长度是14，8是16,3是6，最终该树的带权路径长度之和（wpl）就是26+14+16+6=62。

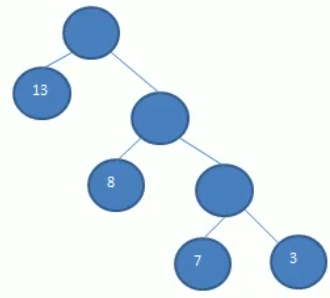
image-20200717165733984

而该树与上图有相同的叶子节点，但是wpl却是13+16+21+9=59，这是拥有这几个相同叶子节点的树里面wpl最小的，所以这颗树就是一颗赫夫曼树。

我们不难看出，赫夫曼树最大的特点：权越大的节点越靠近根节点

二、如何构建赫夫曼树

举个例子，我们要将{6,1,3,7,13,8,29}这一串数列组建为赫夫曼树

  1. 首先，我们对齐从小到大排序，得到{1,3,6,7,8,13,29}

  2. 取出1和3，并以两节点之和4为根节点组建树

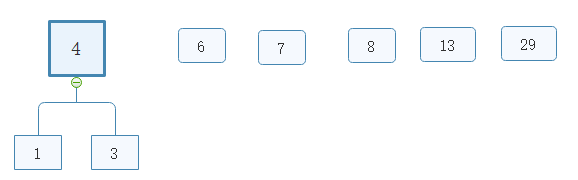
    image-20200717172110379

  3. 取出6，并与4之和10为根节点构建树

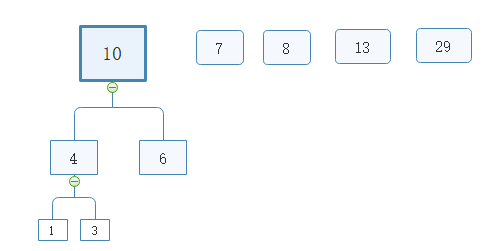
    image-20200717172201798

  4. 取出7，并与10之和17为根节点构建树

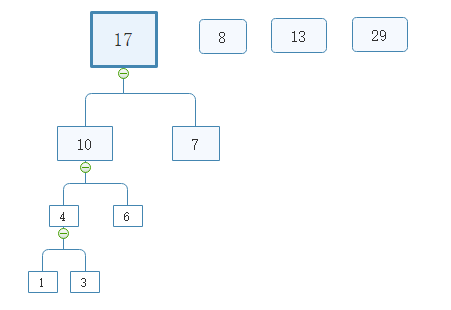
    image-20200717172314477

  5. 重复以上步骤最终得到赫夫曼树

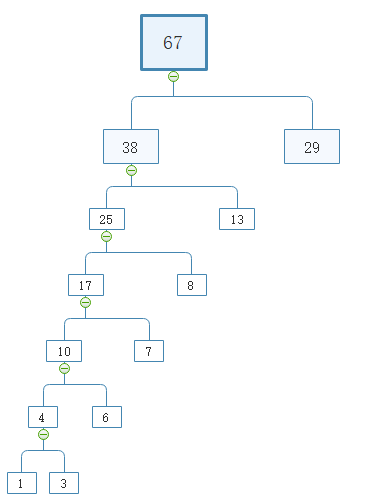
image-20200717172440901

三、代码实现

首先先写一个节点类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * @Author：CreateSequence
 * @Date：2020-07-17 17:31
 * @Description：赫夫曼树使用的节点
 */
public class Node implements Comparable<Node> {

    int val;
    Node left;
    Node right;

    public Node(int val) {
        this.val = val;
    }

    /**
     * 父节点的构造方法
     * @param left
     * @param right
     */
    public Node(Node left, Node right) {
        this.left = left;
        this.right = right;
        this.val = left.val + right.val;
    }

    @Override
    public String toString() {
        return "val=" + val;
    }

    /**
     * 实现排序接口，从大到小
     * @param o
     * @return
     */
    @Override
    public int compareTo(Node o) {
        return -(this.val - o.val);
    }
}

实现一个构造赫夫曼树的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * @Author：CreateSequence
 * @Date：2020-07-17 17:37
 * @Description：赫夫曼树
 */
public class HuffmanTree {
    /**
     * 创建赫夫曼树
     * @param arr
     */
    public static List<Node> createHuffmanTree(int[] arr){
        //将数组元素拆分成节点
        List<Node> nodes = new ArrayList<>();
        for (int i : arr) {
            nodes.add(new Node(i));
        }

        //构建树
        while (nodes.size() > 1) {
            //排序
            Collections.sort(nodes);

            //取出最小的两个数构建树
            Node left = nodes.get(nodes.size() - 1);
            Node right = nodes.get(nodes.size() - 2);
            Node parant = new Node(left, right);

            //删除两个节点
            nodes.remove(left);
            nodes.remove(right);

            //将根节点添加至集合
            nodes.add(parant);
        }

        return nodes;
    }
}
0%