一、什么是多路查找树
二叉树有诸多便利之处,但是当二叉树节点极多时,二叉树的构建速度就会受影响,而且过高的层数也会导致对树的操作效率降低。
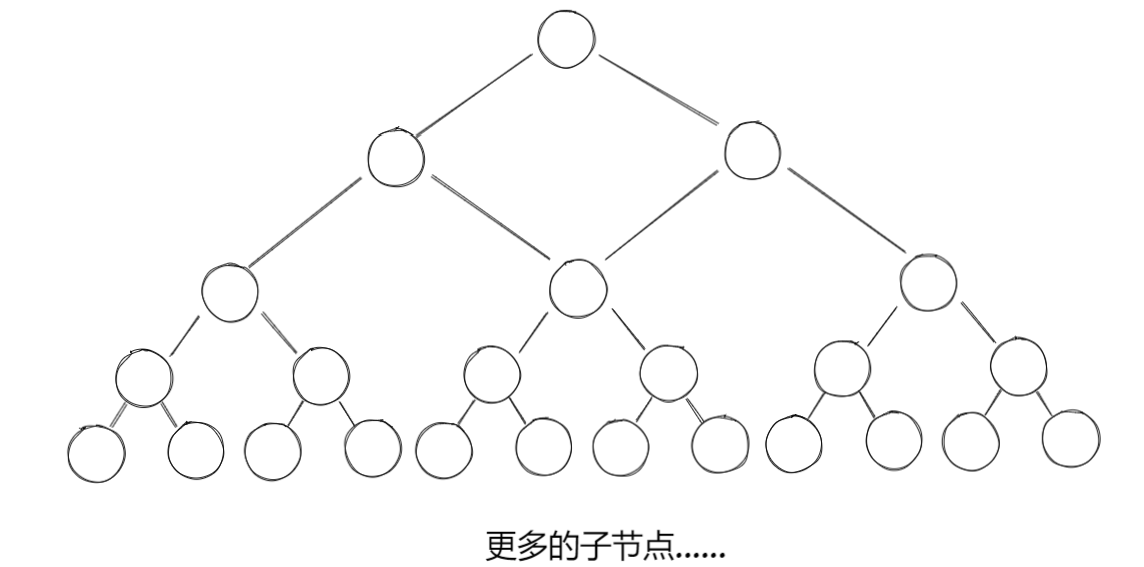
对于树的查找而言,树的高度决定了查找的时间下限,但是同样数量的节点,如果要高度小那每一层容纳的节点就要多,而二叉树每一层固定的节点数导致的高度难以降低,为此每一个节点都能拥有多个子节点的多叉树(multi way tree)就出现了.
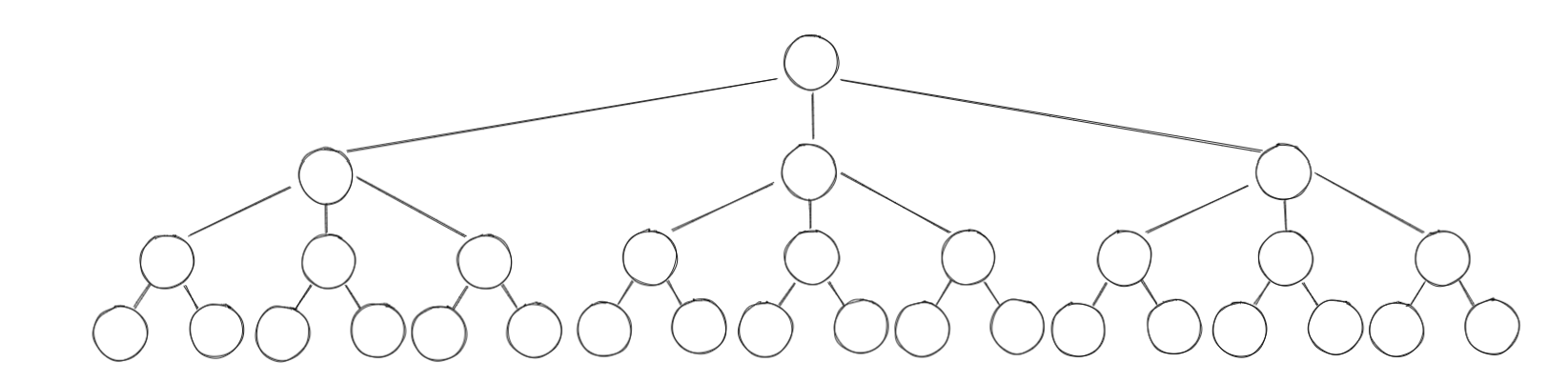
B树,B+树都是多叉树
二、B树
B树也称B-树,它是一颗多路平衡查找树。
2-3树是最简单的B树,它具有以下特点:
- 2-3树的所有叶子节点都在同一层(只要是B树都满足该条件)
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点。三节点本身包含两个数据项
- 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点。二节点本身包含一个数据项
- 2-3树是由二节点和三节点构成的树。
我们以数列{16,24,12,32,14,26,34,10,8,28,38,20}构建2-3树为例:
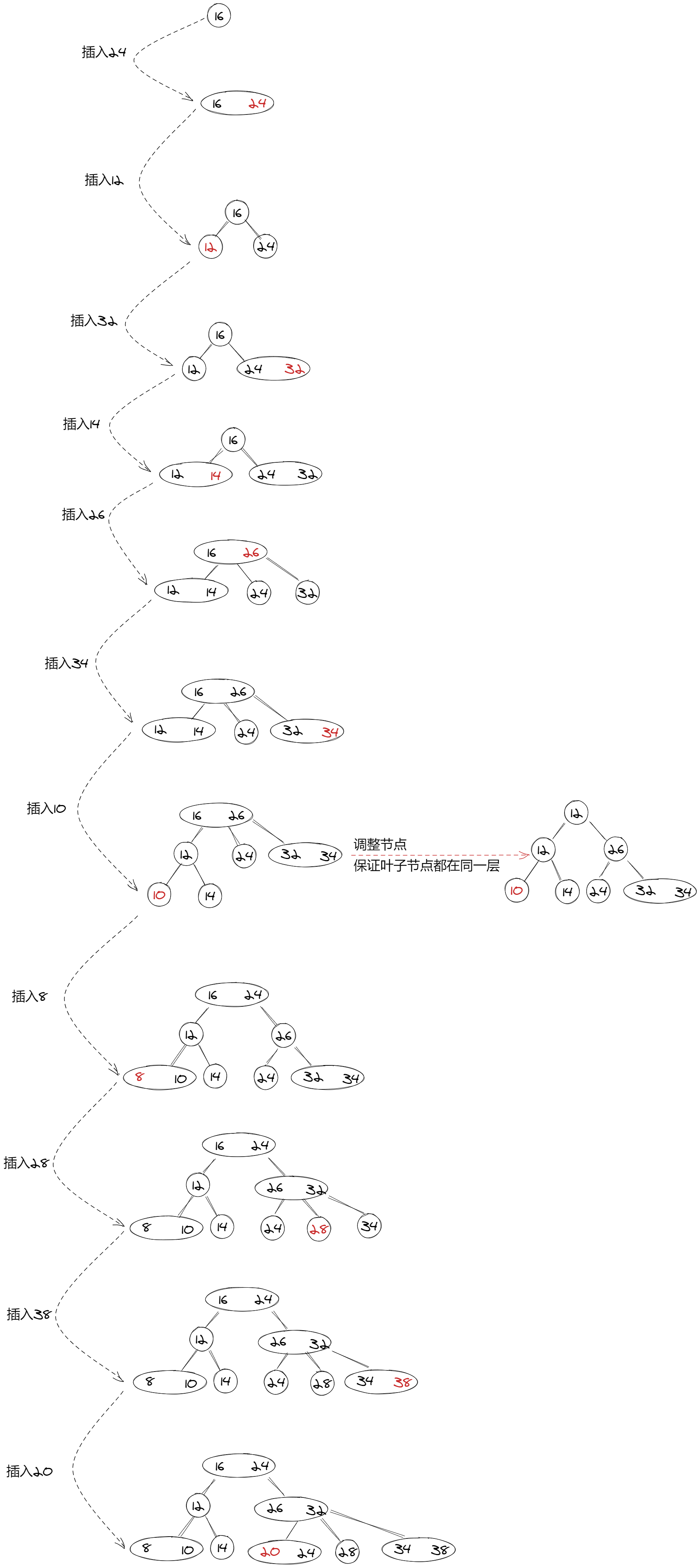
对于2-3树插入的特点,我们举几个具有代表性的例子:
- {16}插入24:由于24大于16,又16是一个二节点,他要么有两个值节点要么没有节点,所以只能插到16节点里,变成一个三节点
- {16,24}插入12:由于12小于16,又[16|24]是一个三节点,所以将[16|12]拆开,以16为父节点,24为右子节点,12作为为左子节点插入
- {16,24,12,32,14,26,34}插入10:按顺序找到[12|14]节点,将三节点拆开后,以12为父节点,14为左子节点,10作为为左子节点插入,由于插入10以后,树的所有叶子节点就不在同一层了,所以需要对其他子树进行调整,将[16|26]拆开,将26变为16的右子节点,原本的24与[32,34]节点变为24的左右子节点
除了2-3树以外,还有一种2-3-4树也是B树的一种,相比2-3树,它多了一个包含能3个数据项与四个子节点的四节点:
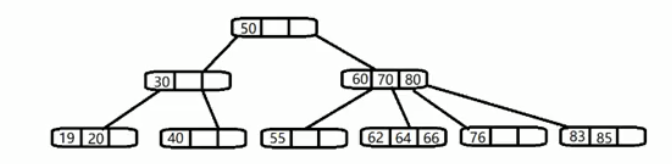
由于B树的关键字集合可以分布在整颗树上,如果查找的数据离根节点很近,此时查找会比B+树快
三、B+树
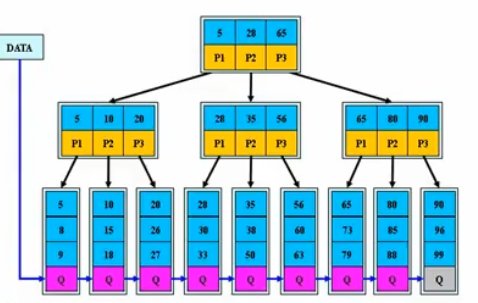
B+树具有以下特点:
- B+树只有叶子节点存放数据(稠密索引),而非叶子节点只作为索引(稀疏索引),这使得非叶子节点所能保存的关键字大大增加
- B+树的叶子节点存放的数据是有序的
相对B树,B+具有以下优点:
- B+树查询速度更稳定:B+所有关键字数据地址都存在叶子节点上,所以每次查找的次数都相同
- B+树的层级更少:相较于B树B+每个非叶子节点存储的关键字数更多,树的层级更少所以查询数据更快;
- B+树天然具备排序功能:B+树所有的叶子节点数据构成了一个有序链表,在查询大小区间的数据时候更方便,数据紧密性很高,缓存的命中率也会比B树高
- B+树全节点遍历更快:B+树遍历整棵树只需要遍历所有的叶子节点即可,而不需要像B树一样需要对每一层进行遍历,这有利于数据库做全表扫描
也由于这些优点,在mysql中,索引实现是基于B+树的。